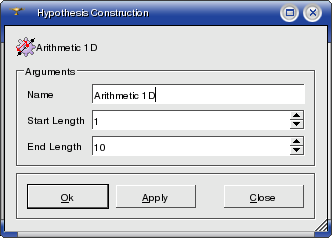

Arithmetic 1D hypothesis allows to split edges into segments with a length that changes in arithmetic progression (Lk = Lk-1 + d) beginning from a given starting length and up to a given end length.


See Also a sample TUI Script of a Defining Arithmetic 1D hypothesis operation.
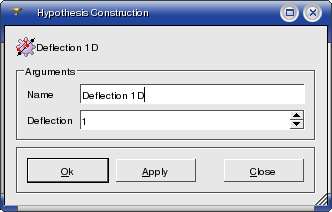
Deflection ID hypothesis can be applied for meshing curvilinear edges composing your geometrical object. It uses only one parameter: the value of deflection.
A geometrical edge is divided into equal segments. The maximum distance between a point on the edge within a segment and the line connecting the ends of the segment should not exceed the specified value of deflection . Then mesh nodes are constructed at end segment locations and 1D mesh elements are constructed on segments.

See Also a sample TUI Script of a Defining Deflection 1D hypothesis operation.
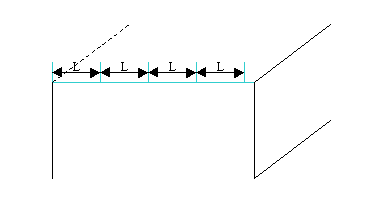
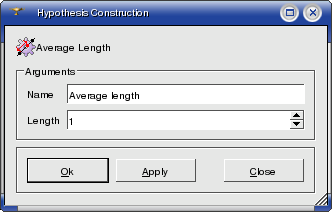
Average Length hypothesis can be applied for meshing of edges composing your geometrical object. Definition of this hypothesis consists of setting the length of segments, which will split these edges. The points on the edges generated by these segments will represent nodes of your mesh. Later these nodes will be used for meshing of the faces abutting to these edges.

See Also a sample TUI Script of a Defining Average Length hypothesis operation.
Number of segments hypothesis can be applied for meshing of edges composing your geometrical object. Definition of this hypothesis consists of setting the number of segments, which will split these edges. In other words your edges will be split into a definite number of segments with approximately the same length. The points on the edges generated by these segments will represent nodes of your mesh. Later these nodes will be used for meshing of the faces abutting to these edges.
You can set the type of distribution for this hypothesis in the Hypothesis Construction dialog bog :
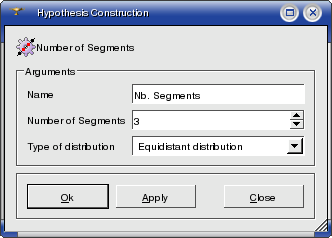
Equidistant Distribution - all segments will have the same length
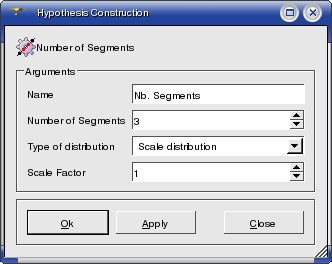
Scale Distribution - each next segment differs from the previous according to the formula: Ai+1 = Ai * k, where k is Scale Factor
 \
\
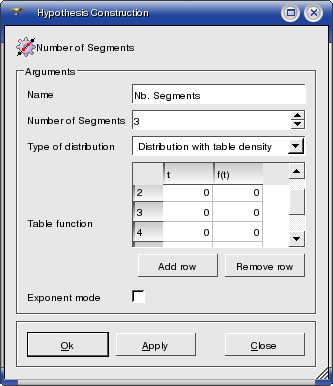
Distribution with Table Density - you input a number of pairs t - F(t) and the program computes the formula, which will rule the change of length of segments.
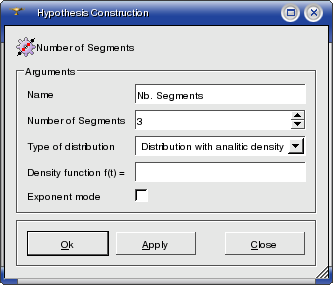
Distribution with Analytic Density - you input the formula, which will rule the change of length of segments
See Also a sample TUI Script of a Defining Number of Segments hypothesis operation.
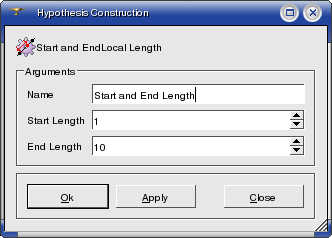
Start and End Length hypothesis allows to divide a geometrical edge into segments so that the first and the last segments have a specified length. The length of each but the first segment differs from length of the previous one by a constant factor. Then mesh nodes are constructed at segment ends location and 1D mesh elements are constructed on them.

See Also a sample TUI Script of a Defining Start and End Length hypothesis operation.