Pattern mapping
About patterns
 The pattern describes a mesh to generate: positions of
nodes within a geometrical domain and nodal connectivity of elements.
As well, a pattern specifies the so-called key-points, i.e. nodes that
will be located at geometrical vertices. Pattern description is stored
in <pattern_name>.smp file.
The pattern describes a mesh to generate: positions of
nodes within a geometrical domain and nodal connectivity of elements.
As well, a pattern specifies the so-called key-points, i.e. nodes that
will be located at geometrical vertices. Pattern description is stored
in <pattern_name>.smp file.
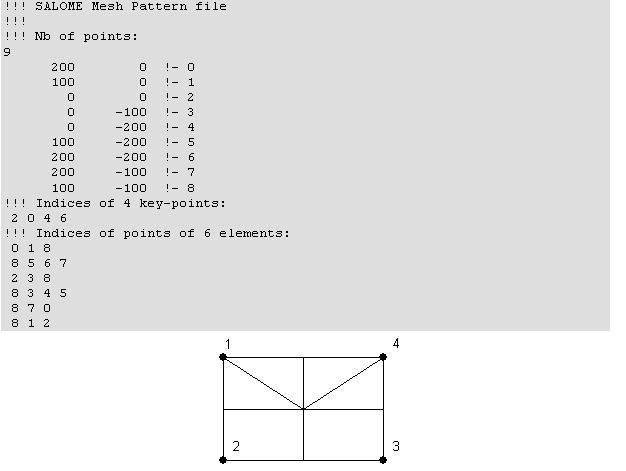
The smp file contains 4 sections:
1. The first line holds the number of nodes
(N).
2. The next N lines describe nodes coordinates.
Each line holds 2 coordinates of a node.
3. A key-points line: indices of nodes to
be mapped on geometrical vertices. An index n refers to a node described
on an n-th line of section 2. The first node index is zero.
4. The rest lines describe nodal connectivity
of elements, one line for an element. A line holds indices of nodes forming
an element. An index n refers to a node described on an n-th line of the
section 2. The first node index is zero. There must be 3 or 4 indices
on a line: only 2d elements are allowed.
The 2D pattern must contain at least one element and at least one key-point.
All key-points must lay on boundaries.
An example of a simple smp file and a preview of a pattern described
in this file:
Application of pattern mapping
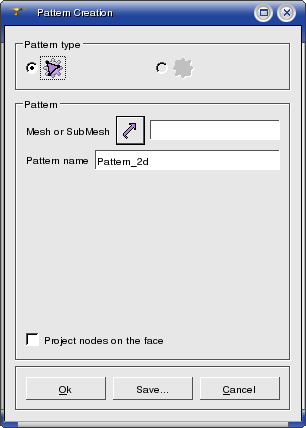
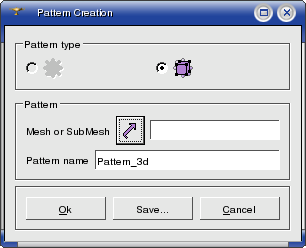
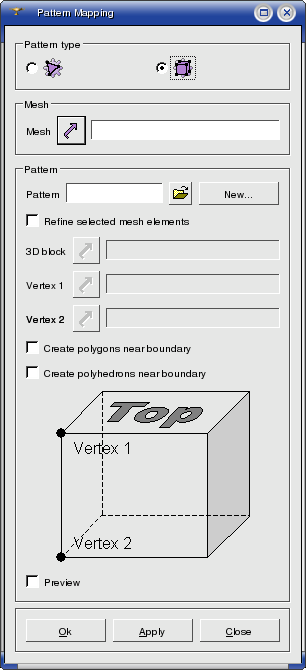
To apply pattern mapping to a geometrical object:
1. From the Modification
menu choose the Pattern Mapping
item or click  button in the toolbar. The following
dialog box shall appear:
button in the toolbar. The following
dialog box shall appear:
To apply a pattern to a geometrical object, you should specify:
- a face having the number of vertices equal
to the number of key-points in the pattern; the number of key-points on
internal boundaries of a pattern must also be equal to the number of vertices
on internal boundaries of a face;
- a vertex to which the first key-point should
be mapped,
- reverse or not the order of key-points.
(The order of vertices of a face is counterclockwise looking from outside).
Then you either load a .smp pattern file previously created manually
by clicking on the  button, or click on the New
button for automatic generation.
button, or click on the New
button for automatic generation.
For an automatic generation you just specify a geometrical face having
a mesh built on it. Mesh nodes lying on face vertices become key-points.
Additionally, you may choose the way of getting nodes coordinates by projecting nodes on the face instead
of using "positions on face" generated by mesher (if there is
any). Faces having a seam edge canít be used for automatic pattern creation.
When creating a pattern from an existing mesh, there are two possible
cases:
1. A sub-mesh on face is selected. A pattern is created from the 2d
elements bound to a face by mesher. Node coordinates are either "positions
on face" computed by mesher, or coordinates got by node projection
on a geometrical surface, according to your choice.
2. A mesh where the main shape is a face, is selected. A pattern is
created from all the 2d elements in a mesh. If all mesh elements are build
by mesher, the user can select the way of getting nodes coordinates, else
all nodes are projected on a face surface.
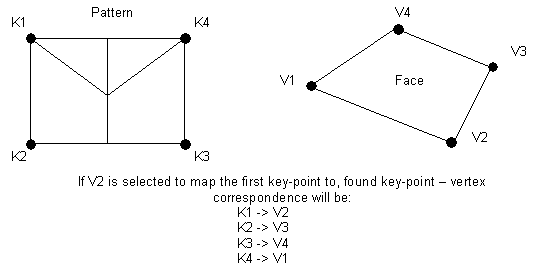
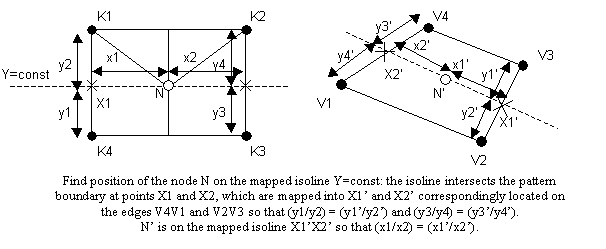
Mapping algorithm:
The mapping algorithm is as follows:
1. Key-points are set in the order that they
are encountered when walking along a pattern boundary so that elements
are on the left. The first key-point is preserved.
2. Find geometrical vertices corresponding
to key-points by vertices order in a face boundary; here, "Reverse
order of key-points" flag is taken into account.
3. Boundary nodes of a pattern are mapped
onto edges of a face: a node located between certain key-points on a pattern
boundary is mapped on a geometrical edge limited by corresponding geometrical
vertices. Node position on an edge reflects its distance from two key-points.

4. Coordinates of a non-boundary node in
a parametric space of a face are defined as following. In a parametric
space of a pattern, a node lays at the intersection of two iso-lines,
each of which intersects a pattern boundary at least at two points. Knowing
mapped positions of boundary nodes, we find where isoline-boundary intersection
points are mapped to, and hence we can find mapped isolines direction
and then, two node positions on two mapped isolines. The eventual mapped
position of a node is found as an average of positions on mapped isolines.
 The pattern describes a mesh to generate: positions of
nodes within a geometrical domain and nodal connectivity of elements.
As well, a pattern specifies the so-called key-points, i.e. nodes that
will be located at geometrical vertices. Pattern description is stored
in <pattern_name>.smp file.
The pattern describes a mesh to generate: positions of
nodes within a geometrical domain and nodal connectivity of elements.
As well, a pattern specifies the so-called key-points, i.e. nodes that
will be located at geometrical vertices. Pattern description is stored
in <pattern_name>.smp file.
 button in the toolbar. The following
dialog box shall appear:
button in the toolbar. The following
dialog box shall appear:
 button, or click on the
button, or click on the